Download

Welcome to SOFiA

Who is behind SOFiA

Feature overview

System overview

Function reference

readVSAdata

mergeArrayData

F/D/T

gauss

lebedev

S/W/G

S/T/C

W/G/C

S/F/E

M/F

R/F/I

P/D/C

I/T/C

makeMTX

makeIR

visual3D

Coordinate System

Application Examples

Example 1

Example 2

Example 3

Example 4

Example 5

Example 6

Example 7

Example 8

Array Datasets

VariSphear system

Groups and Mailinglists

Contact and Support

How to Reference

SOFiA Modal Radial Filters

SOFiA M/F is a modal radial filter core for spherical microphone arrays. M/F can generate filters for different sphere and microphone configurations and involves soft-limiting of the mode amplification and free field powerloss compensation.

ARGUMENTS

Input

Output

Definitions

The d,,n,, coefficients are defined as:

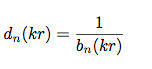
Where b,,n,, depends on the sphere configuration and microphone type:

AC0 Open sphere with pressure transducers:

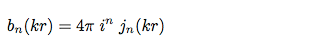
AC1 Open sphere with pressure gradient transducers (cardioids):

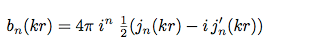
AC2 Rigid sphere with pressure transducers:


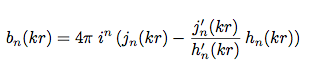
Configurations AC3 and AC4 are contributed and implemented by Nils Peters:

AC3 Rigid sphere with pressure gradient transducers (cardioids):

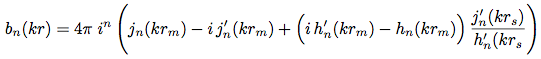
AC4 Dual open sphere with pressure transducers:

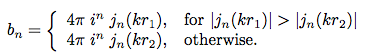
j,,n,,(kr) denotes the spherical bessel function of the first kind, h,,n,,(kr)
the spherical hankel function of the second kind and i=sqrt(-1).

When modal amplification limiting is enabled, d,,n,, is defined as:

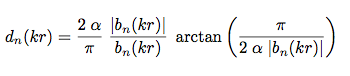
Powerloss free-field filters:

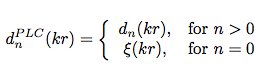
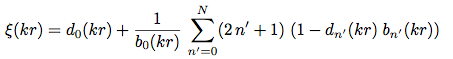
BASIC RADIAL FILTERS

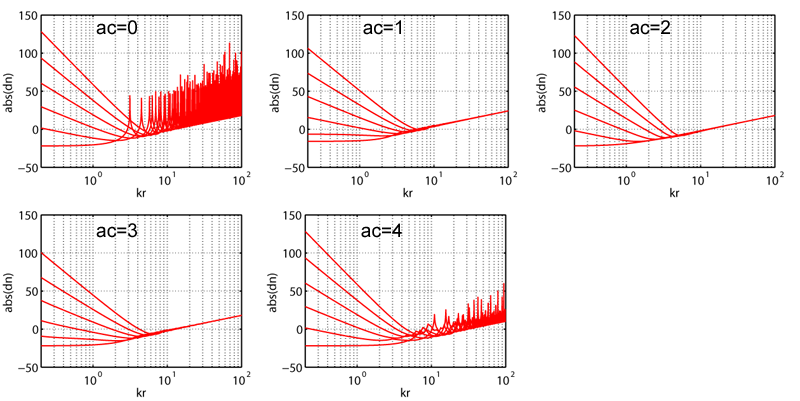
The plots show basic radial filters (no limiting, no plc) for N=5 and different array configurations (ac): ac=0 Open Sphere with pressure transducers, ac=1 Open Sphere with pressure gradient transducers (cardioid), ac=2 Rigid Sphere with pressure transducers, ac=3 Open Sphere with gradient transducers (cardioid) and ac=4 Dual Open Sphere with pressure transducers.

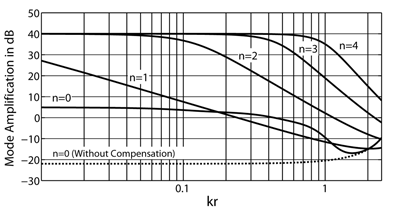
SOFT-LIMITING OF THE MODE AMPLIFICATION

At low kr the modes have to be amplified very hard (see figure above). In real array datasets this required amplification cannot be achieved as the singnal to noise ratio is limited. Strong amplification would raise more noise then useful signal contribution and disturb the array output signal. Therefore the mode amplification has to be limited to reasonable values in real life. This should not be done with hard limits as hard limiting leads to artifacts in the spatial domain. SOFiA M/F therfore uses soft-knee limitation.

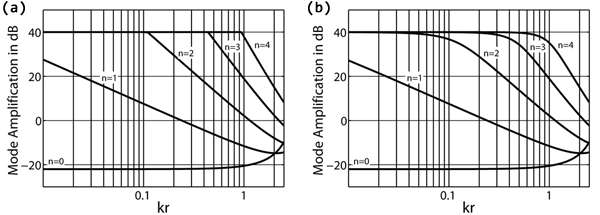
The left figures (a) show hard limiting and the right ones (b) soft limiting. Both filtersets are limited to to +40dB

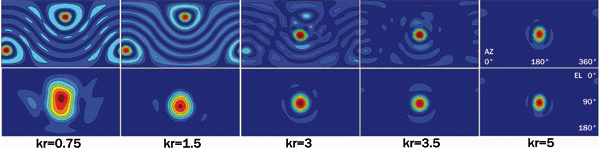
The following figure shows a real measured array response to a plane wave with basic radial filters in the upper row and SOFiA soft-limited radial filters in the bottom row. The response for low kr using basic radial filters is disrupted due to measurement noise. The soft-limited response looses directivity (as expected) but keeps stable.

BEAM RESPONSE

The modal amplification limiting has influence on the kr-response (which can be seen as the array's frequency response). The kr-response can be controlled by plotting the return vector beam e.g. with semilogx(20*log10(abs(beam'))).

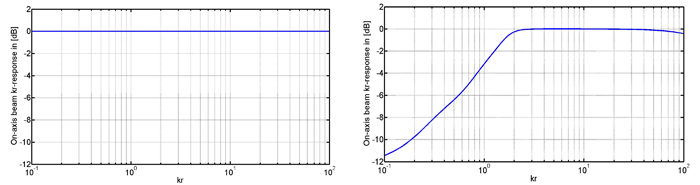
FREE FIELD PLC

In a free field the kr-response can be aligned using the N0 mode which offers a good signal to noise ratio. This is called plc (powerloss compensation). The plc leads to a perfect on-axis kr-response. The plc compensation can be applied to the full spectrum or be limited to low frequencies only. In the last case M/F will fade the compensated filter to normal N0 filters at their minimum distance.

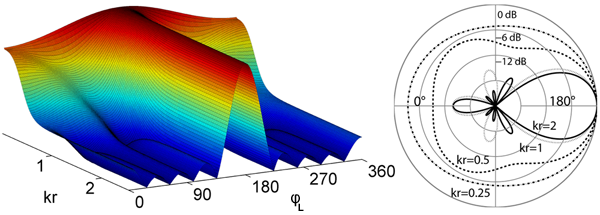
The figure shows the array's azimutal response to a full kr-spectrum plane wave coming from 180°C. The response is compensated on axis but other directions have a raised sensitivity to low frequencies. This leads to an over-emphasized low frequency response in diffuse fields.

FILE(S):

HEADER

The M/F core involves Bessel and Hankel functions provided by the peer-reviewed BOOST C++ Math Library under the BOOST Software License.